Вам назначили интервью в Т-Банк. Первая радость сменилась лёгкой паникой: «А что там будут спрашивать?». Однако подготовиться к интервью вполне возможно.
Андрей Ткаченко, аналитик данных в X5 Group, разобрал задачи на техническом интервью на позицию аналитика данных в Т-Банке. Благодаря ему вы научитесь решать ключевые задачи по SQL и Python, которые являются решающим фильтром для кандидатов.
Этапы отбора в Т-Банк
Вне зависимости от того, на какую позицию вы собеседуетесь, процесс един для каждой команды и вы всегда можете быть готовы к следующему этапу.
- HR-скрининг. Рекрутер и кандидат созваниваются по телефону, вы отвечаете на базовые вопросы про опыт и пожелания к новому месту работы и договариваетесь о времени технического интервью.
- Техническое интервью. Здесь проверяют всё и сразу. Вопросы начинаются от самой базы и растут по ходу интервью. Если уверенно и подробно рассказывать, как и почему что-то работает, то часть вопросов могут пропустить.
Но не удивляйтесь, когда на интервью для опытных сотрудников вам придётся рассказывать, как суммировать строки в SQL. На всё про всё час, а на самом деле выйдет минут 40-45.
- Знакомство с командами. Возможно, на встречу придёт только лидер команды, куда вы договаривались прийти изначально, но бывают случаи, когда приходят коллеги из других отделов и даже могут предложить условия лучше.
- Проверка службы безопасности, оффер и онбординг.
В этой статье мы подробно рассмотрим второй пункт.
Как это принято в компаниях с отлаженными процессами, вас будет собеседовать человек, который вообще про вас ничего не знает. А вернее, знает он лишь то, что он должен вас хорошо проверить, потому что именно ему сообщать HR и лидерам команд о вашей технической составляющей. Но не забывайте и про софт-скиллы.
Собеседование делится на три части: SQL, Python, математическая статистика и теория вероятностей.
SQL
Для примера будем работать с витриной транзакций user_money:
date— datetime, дата;id— string, айди клиента;money_movement— int, движение денег: с минусом списание, с плюсом пополнение;money_movement_type— string, тип движения. Банкомат, приложение банка, сторонние сервисы. В типах могли бы быть и подтипы, но в контексте задач опустим эти детали.
Задача 1. Посчитать, сколько денег внёс на карту через банкомат каждый из клиентов за календарный месяц.
select date, id,
sum(money_movement) sum_add_money
from user_money
where money_movement_type = 'bankomat' and money_movement > 0
group by date, id, date_trunc(‘month’, date) as mnth
Что мы сделали? Для каждого месяца и клиента посчитали сумму денег с типом движения «банкомат» и положительным (+) знаком. Из тонкостей тут лишь то, что можно поспешить и не указать, что нам нужно лишь пополнение.
Например, у вас есть три активности по банкомату: +1 000, +500, -10 000. Не указав маленькую деталь, вы могли бы получить, что было внесено -8 500 рублей.
Задача 2. Теперь нам нужно определить топ-10 по сумме внесённых денег за месяц:
select date, id,
sum(money_movement) sum_add_money
from user_money
where money_movement_type = 'bankomat' and money_movement > 0
group by date, id
order by sum_add_money desc
limit 10
Здесь несложно — добавляем сортировку и лимит по строкам, чтобы было ровно столько, сколько нам нужно. Все даты урезаны до первого дня месяца. То есть 15.04.2025, 17.04.2025, 11.04.2025 — всё станет 01.04.2025.
Задача 3. Узнаём, что у нас есть ещё одна витрина — история версий приложения по клиентам.
mobile_app_history:
id— string;install_time— date;uninstall_time— date;app_version— string.
Какая версия приложения стояла у клиента Х в день Y, когда он переводил деньги?
select
um.date,
um.id,
mah.app_version
from user_money um
left join mobile_app_history mah on um.id = mah.id and date between install_time and uninstall_time
where date = X and um.id = Y and money_movement < 0
Итак, мы узнали, какой версией приложения пользовался клиент в день когда совершал переводы. Можно было ошибиться, попробовав объединять по дате, равной дате перевода, но это неверный путь. Приложение устанавливается и используется без изменений несколько месяцев, а то и больше.
Тут нам нужно догадаться, что актуальная версия приложения у нас лежит между датами установки и удаления. Совпадать они не могут, так как после установки приложения нужно хотя бы пара секунд для активации, а значит, активация и тем более перевод будут позже. А если бы вы захотели в момент перевода приложение удалить, то ему всё равно потребовалось бы время на закрытие. Так что дата транзакции точно будет меньше даты удаления.
Python
Переходим к Python-части.
Вопрос 1. Какие типы данных есть в Python?
Численные:
- int — целые числа (10, 2, 123456)
- float — числа с плавающей точкой (10.12, 0.5, 456.987423). Тут важно отметить, что 1 + 1 == 2 — это False, и всё дело как раз в плавающей запятой. Мы можем не увидеть, но сотый знак после запятой у этих двух единиц и у двойки будет отличаться. А так как знаки после запятой не равны, 1+1 != 2.
- complex — комплексные числа (1 + 2j, мнимая единица).
Строки:
- str ("2", "Привет!")
- Булево значение: 1 или 0, где 1 — True и 0 — False. Например, значение 1 в поле subscribe говорит о наличии подписки, 0 — об её отсутствии.
Списки: list (1, 2, 3, "Чатыри").
Кортежи: tuple (10, 20, "апельсин").
Словари: dict ('name': "Sergey", 'age': 40). Обращаясь к словарю по аргументу name, мы получим "Sergey".
Множества: set ({1, 2, 3, 4, 0})
Есть ещё специальные типы, и можно просто сказать, что мы про них знаем, но ими не пользуемся.
Вопрос 2. А чем эти типы отличаются?
- Изменяемость vs неизменяемость: списки, словари и множества изменяемы, тогда как строки, кортежи и числа неизменяемы.
- Порядок элементов: списки и кортежи сохраняют порядок следования элементов, тогда как словари и множества — нет.
- Индексация: строки, списки и кортежи индексируемы, словарь доступен по ключу, множества вообще не имеют индексов.
- Уникальность элементов: в списке и словаре элементы могут повторяться, в множестве повторения невозможны.
Вопрос 3. Напишите функцию, которая на ввод принимает одно число и возвращает "simple", если оно простое и "not a simple", если не простое.
Нужно вспомнить, что такое простое число. Это число, которое делится без остатка только на единицу и само на себя, Единица простым числом не считается.
Например, 2 простое, 3 простое, 4 не простое, 7 простое, 9 не простое.
Сам код:
def is_prime(n):
if n <= 1:
return "not a simple"
for i in range(2, int(n * 0.5) + 1):
if n % i == 0:
return "not a simple"
return "simple"
Что делает код: мы принимаем число n и проверяем, чтобы оно было больше 1. Если условие не пройдено, возвращаем "not a simple". Итерационно проходимся от 2 до n/2 (n 0.5), и добавляем единицу, чтобы верхняя граница нашего интервала не была меньше половины от числа.
Почему n/2? Рассмотрим на примере числа 30. Оно не простое — если до 15 (30/2) оно не поделилось без остатка, то и после 15 не поделится без остатка. А вот на 15 прекрасно делится: 30/15 = 2.
n % i == 0 — проверяем, что остаток от деления не равен нулю. Если равен, число не простое.
Мы проверили, что наше число больше 1, не делится без остатка в интервале от 2 до n/2, а само на себя делится любое число. Если все условия выполнены, return "simple".
Статистика и теория вероятностей
Мы прошли часть интервью по Python и после небольшого разбора (рассказа, что делает код) переходим к секции «Матстат и теория вероятностей».
Как уже обсуждалось, на всё интервью есть час, без приветствия и смолтолка около 45-50 минут. Порядка 35 минут было потрачено только на тех часть и пояснения, почему всё так, поэтому на статистику осталось времени проверить только самую базу.
Вопрос 1. Что такое нормальное распределение?
Нормальное распределение (или Гауссово распределение) — это симметричное колоколообразное распределение значений случайной величины вокруг среднего значения. Оно характеризуется двумя параметрами: средним значением (μμ) и стандартным отклонением (σσ).
Важность нормального распределения заключается в центральной предельной теореме, согласно которой сумма большого числа независимых случайных величин стремится распределяться нормально независимо от исходных распределений каждой отдельной величины. Это позволяет применять нормальность даже тогда, когда отдельные наблюдения имеют неизвестное распределение.
Вопрос 2. Как почистить данные, имеющие нормальное распределение от выбросов?
Чтобы очистить данные с нормальным распределением от выбросов, рекомендуется использовать метод удаления точек, выходящих за пределы интервала трех сигм (правило трёх сигм):
- Рассчитайте среднее значение (μμ) и стандартное отклонение (σσ) вашей выборки.
- Определите границы диапазона, исключающего выбросы: [μ−3σ, μ+3σ][μ−3σ, μ+3σ].
- Удалите все точки, лежащие вне указанного диапазона.
Таким образом, остаются только те данные, которые находятся в пределах трёх стандартных отклонений от среднего значения. Такой подход эффективен благодаря свойствам нормального распределения, согласно которым около 99.7% всех данных лежат внутри границ трёх сигм.
А как же рассчитать стандартное отклонение? Это корень из квадрата суммы разниц каждого наблюдения от среднего в этой группе, поделённых на количество наблюдений.
Расчёт проводится по следующей формуле:
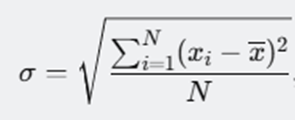
где:
- σ — стандартное отклонение;
- xi — отдельное наблюдение;
- x‾ — среднее арифметическое выборки;
- NN — число наблюдений.
А почему квадрат? Квадрат нужен, чтобы избавиться от знаков. После возведения в квадрат у нас все значения будут положительными.
Вопрос 3. Какие существуют методы проверки гипотезы о среднем значении выборки?
Для проверки гипотезы о среднем значении выборки используются два основных подхода:
- T-тест (Student's t-test) применяется, когда размер выборки небольшой (< 30) и неизвестно истинное значение стандартного отклонения генеральной совокупности. Этот тест основывается на предположении, что распределение выборочных средних подчинено распределению Стьюдента. Статистика теста рассчитывается как отношение разницы между средним выборочным значением и нулевым гипотетическим средним к стандартной ошибке выборочного среднего. Далее эта статистика сравнивается с критическими значениями распределения Стьюдента.
Что за критические значения? Проще всего их посмотреть в таблице критических значений. Для этого нам необходим уровень значимости, обычно это 0.05 и число степеней свободы = количество наблюдений (статистик) в выборке -1. Для группы из 20 наблюдений число степеней свободы = 19. Критические значения — это значения, с которыми мы будем сравнивать наши результаты. Если наш результат больше чем в таблице, группы разные, в обратном случае — нет.
- Z-тест (z-test) используется, когда известно точное значение стандартного отклонения генеральной совокупности либо когда размер выборки достаточно большой (обычно > 30). Z-статистика рассчитывается аналогично t-тесту, но теперь среднее сравнивается с известным стандартным отклонением генеральной совокупности. Полученная z-статистика проверяется относительно таблицы стандартных нормальных распределений.
Различия между этими методами заключаются главным образом в выборе критерия оценки (распределение Стьюдента vs нормальное распределение) и размере выборки.
